Matriks
Pengertian Matriks
Matriks adalah susunan bilangan real (kompleks) berbentuk empat persegi panjang yang dibatasi oleh tanda kurung.
Secara umum sebuah susunan bilangan yang disebutkan di atas biasanya tersusun atas baris atau m dan kolom. Kemudian ada pula yang dinamakan ordo.
Ordo adalah ukuran suatu matriks yang ditunjukkan oleh jumlah baris dan kolomnya.
Ordo = m x n
Istilah-istilah :
Lambang matrik digunakan huruf besar, A, B, C
Elemen matrik digunakan lambang huruf kecil, a. b , c …
Bagian mendatar disebut baris
Bagian tegak disebut kolom Indeks-I menyatkan baris,
indeks-j menyatakan kolom Jumlah baris=m, jumlah kolom=n
Ukuran matrik disebut ordoMatrik dengan jumlah baris=m, jumlah kolom=n diebut dengan ukuran (mxn) atau matrik berordo (mxn).
Jenis Matriks :
1. Baris, hanya mempunyai satu baris. Ordonya yakni 1×n dengan jumlah kolom sebanyak n.
2. Kolom, hanya mempunyai satu kolom.Ordonya yakni m×1 dengan jumlah baris sebanyak m.
3. Matriks Persegi adalah matriks yang memiliki banyak baris dan kolom yang sama. Secara umum matriks persegi berordo m x m dapat dinotasikan sebagai A = [aij]m×m
4. Segitiga, matriks persegi dengan elemen di bawah atas atau di atas diagonal bernilai 0.
* Matriks segitiga atas
Matriks segitiga atas merupakan matriks yang semua elemen dibawah diagonal utamanya adalah bilangan 0.

Matriks segitiga bawah merupakan matriks yang semua elemen diatas diagonal utamanya adalah bilangan 0.

bagiannya kecuali diagonal. Contoh:
6. Matriks Nol, seluruh elemennya 0.. Matriks nol dinotasikan dengan O.
7. Matriks diagonal, adalah matriks dimana semua elemen diluar diagonal utamanya adalah 0 dan minimal ada satu elemen pada diagonal utamanya bukan 0.
Contoh A :
8. Matriks skalar adalah matriks diagonal dimana elemen pada diagonal utamanya bernilai sama tetapi bukan satu atau nol.
9. Matriks Baris adalah matriks yang terdiri dari suatu baris
Contoh : A = ( 1 3 4 9 )
10. Matriks Kolom adalah matriks yang terdiri dari satu kolom.
11. Matriks mendatar adalah matriks yang banyaknya baris kurang dari banyaknya kolom.
12. Matriks Tegak adalah matriks yang banyaknya baris lebih dari banyaknya kolom.
13. Matriks Skew Simetris adalah matriks persegi yang apabila ditransposkan akan sama dengan negatif dari matriks semula.
14. Tranpose
Tranpose artinya perpindahan. Dalam materi ini, yang disebut transpose adalah memindahkan baris dengan kolomnya.
Berarti, jika ordo 4 x 3 berarti menjadi 3 x 4. Lambang tranpose adalah huruf t di bagian atas nama matriksnya. Matriks A transpose, misalnya dilambangkan dengan At.
Contoh:
 |
maka matriks transposenya (At) adalah
15. Matriks Simetris
Matriks kotak A disebut simetris jika A = AT
Contoh matriks simetris
Operasi Aritmatik Matriks
1. Penjumlahan Dua Buah Matriks
Dua buah matriks dapat dijumlahkan asalkan memiliki ukuran yang sama. Hasil penjumlahan dua buah matriks menghasilkan sebuah matriks baru yang berukuran sama dengan matriks yang dikalikan.
Operasi penjumlahan dan pengurangan dalam matriks sama, hanya perlu mengganti operator + dengan operator -.
2. Perkalian Dua Buah Matriks
Perkalian pada matriks barangkali sedikit lebih rumit dibandingkan dengan penjumlahan. Dua buah matriks dapat dikalikan jika jumlah kolom matriks pertama sama dengan jumlah baris matriks kedua.
3. Perkalian Matriks Dengan Skalar
Perkalian matriks dengan skalar artinya mengalikan setiap elemen pada matriks dengan nilai skalar yang kita tentukan.
Contoh Perkalian Matriks Dengan Skalar:
Misalkan k adalah sebuah skalar.
4. .Penjumlahan Matriks
Matriks dengan jumlah baris 3 dan kolom 4 hanya bisa dijumlahkan dengan matriks dengan jumlah baris 3 dan kolom 4. Matriks dengan jumlah baris 3 dan kolom 4 tidak bisa dijumlahkan dengan matriks dengan jumlah baris 4 dan kolom 3. Kesimpulannya, jumlah baris dan kolom antar dua matriks yang akan dijumlahkan harus sama.
.
5.Pengurangan Matriks
Seperti halnya operasi hitung penjumlahan matriks, syarat agar dapat mengurangkan elemen-elemen antar matriks adalah matriks harus memiliki nilai ordo yang sama.
DETERMINAN
Determinan adalah nilai yang dihitung dari unsur-unsur sebuah matriks persegi. Matriks persegi sendiri adalah matriks yang memiliki banyak baris dan kolom yang sama, sehingga bentuknya terlihat seperti persegi. Cara menentukan determinan matriks akan berbeda pada tiap ordo.
a. Determinan Matriks Berordo 2 x 2
Rumusnya : Det (A) = |A| = ad – bc
Contoh :
Jawab : Det (A) = |A| = ad – bc
|A| = (2 x 3) – (5 x 4)
|A| =6 -20
|A| =14
b. Determinan Matriks Berordo 3 x 3
Matriks berordo 3×3 adalah matriks berbentuk persegi dengan banyak kolom dan baris sama yaitu tiga.Terdapat dua cara untuk menentukan determinan matriks berordo 3×3, yaitu metode sarrus dan metode minor-kofaktor.
1. METODE SARRUS
Ciri khas metode ini adalah pola perkalian menyilang elemen matriks.
Contoh soal:
Agar lebih mudah, kita tulis kembali elemen-elemen pada kolom ke-1 dan ke-2 di sebelah kanan matriks A sebagai berikut:
Kemudian, tarik garis putus-putus seperti gambar di atas. Kalikan elemen-elemen yang terkena garis putus-putus tersebut. Hasil kali elemen yang terkena garis putus-putus berwarna biru diberi tanda positif (+), sedangkan hasil kali elemen yang terkena garis putus-putus berwarna oranye diberi tanda negatif (-).
2. METODE MINOR- KOFAKTOR
Berdasarkan rumus minor-kofaktor di atas, determinan matriks A dapat dicari dengan menghitung jumlah seluruh hasil kali antara kofaktor matriks bagian dari matriks A dengan elemen-elemen pada salah satu baris atau kolom matriks A. Jadi, pertama, kita pilih salah satu baris atau kolom matriks A untuk mendapatkan nilai determinannya. Misalnya, kita pilih baris ke-1. Elemen-elemen matriks baris ke-1, yaitu a11, a12, dan a13.
Selanjutnya, karena kita pilih elemen-elemen pada baris ke-1, rumus determinan matriks yang kita gunakan adalah sebagai berikut:
Langkah kedua, kita cari kofaktor matriks bagian dari matriks A (Cij). Cij = (-1)i+j Mij dan Mij = det Aij dengan Aij merupakan matriks bagian dari matriks A yang diperoleh dengan menghilangkan baris ke-i dan kolom ke-j.
Sebelumnya, kita telah memilih elemen-elemen pada baris ke-1, yaitu a11, a12, dan a13. Oleh karena itu, matriks bagian dari matriks A nya adalah A11, A12, dan A13.
· A11 diperoleh dengan menghilangkan elemen-elemen pada baris ke-1 dan kolom ke-1.
· A12 diperoleh dengan menghilangkan elemen-elemen pada baris ke-1 dan kolom ke-2.
· A13 diperoleh dengan menghilangkan elemen-elemen pada baris ke-1 dan kolom ke-3.
Sehingga,
C. Determinan Matriks Berordo 4x4
1. Determinan Metode EKSPANSI LAPLACE
Andaikan, A=[ ] (nxn) adalah matrik bujur sangkar berordo (nxn), dan = adalah kofaktor elemen matrik A baris ke-i kolom ke-j.
a. Untuk n = 1,
Det(A) = [A]=[ ]=
Untuk, n determinan matrik A diberikan oleh,
b. Det(A) = ; i = 12,....., n
= + +....+ ( Ekspansi kofaktor baris ke-i )
c. Det(A) = ; j = 1,2,......, n
= + +......+ ( Ekspanse kofaktor kolom ke – j.
CONTOH :
Penyelesaian :
= a31C31 + a32C32 + a33C33
= a31(-1)3+1M31 + a32(-1)3+2M31 + a33(-1)3+3M31
= a31M31 – a32M31 + a33M31
= 3[6(8)-0(6)] – 2[0(8)-8(0)] + 2[0(6)-8(6)]
= 144 – 0 – 96
Ekspansi kofaktor baris
Ekspansi kofaktor kolom
2. Cara menghitung determinan (A) dengan metode sarrus (Ordo 4×4)
Masih dengan ciri khas perkalian menyilang milik Sarrus.
Pola pertama dimulai tanda + (plus) dengan aturan 1 – 1 – 1
Pola berikutnya dimulai tanda – (minus) dengan aturan 1 – 2 – 3
Pola terakhir dimulai tanda + (plus) dengan aturan 2 – 1 – 2
Maka, nilai determinan adalah jumlah dari ketiga pola yang dijelaskan di atas, yaitu:
Det A = A1 + A2 + A3
CONTOH SOAL :
penyelesaian : menggunakan baris ke-4 kolom ke-4
dan terbukti kalau hasilnya sama yaitu 8.
1.
DETERMINAN : METODE CHIO
Determinan
matriks A biasanya dinyatakan oleh |A| atau det(A). Terdapat beberapa metode
yang digunakan untuk menentukan determinan matriks yaitu metode Sarrus,
Ekspansi Kofaktor, dan Kondensasi (Penyusutan) CHIO. Kondensasi CHIO merupakan
salah satu metode yang dapat digunakan dalam menentukan determinan matriks yang
memiliki ordo n x n dengan n≥3.
Kondensasi CHIO menyusutkan determinan matriks ordo n x n menjadi ordo (n-1)x(n-1) .
untuk matriks dengan
ordo 3x3. Persamaan yang digunakan untuk metode CHIO ini sebagai berikut:
Selanjutnya untuk
matrik dengan ordo 4 x 4. Persamaan yang digunakan untuk metode CHIO ini
sebagai berikut:
Apabila ukuran
matriksnya diperluas menjadi n x n, maka diperoleh persamaan untuk metode CHIO
adalah sebagai berikut:
Contoh 1 :
Contoh 2 :
2.
SIFAT-SIFAT DETERMINAN
1. Jika A adalah sebarang matriks kuadrat
yang mengandung sebaris bilangan nol, maka det(A) = 0.
2. Jika A adalah matriks segitiga n x n, maka det(A) adalah hasil kali entri-entri pada diagonal utama, yakni det(A) = a11a22 … ann
3. Misalkan A’ adalah matriks yang
dihasilkan bila baris tunggal A dikalikan oleh konstanta k, maka det(A’) = k
det(A).
4. Misalkan A’ adalah matriks yang
dihasilkan bila dua baris A dipertukarkan, maka det(A’) = -det(A).
5. Misalkan A’ adalah matriks yang
dihasilkan bila kelipatan satu baris A ditambahkan pada baris lain, maka
det(A’) = det(A).
6. Misalkan A, A’ dan A” adalah matriks n x
n yang hanya berbeda dalam baris tunggal, katakanlah baris ke-r, dan anggap
bahwa baris ke r dari A” dapat diperoleh dengan menambahkan entri-entri yang
bersesuaian dalam baris ke-r dari A dan dalam baris ke-r dari A’, maka det(A”)
= det(A) + det(A’) [hasil yang serupa juga berlaku untuk kolom]
3. METODE CROUT
Adalah mendekomposisi
suatu matriks untuk memperoleh elemen diagonal utama matriks segitiga atas (U)
bernilai satu elemen lainnya
rumus dari metode crout
sebagai berikut:
Langkah-langkah yang harus dilakukan pada
Metode Reduksi Crout adalah :
Didapatkan persamaan
sehingga rumusnya :
Contoh soal metode crout :
4. Determinan matrik dengan metode dekomposisi
Dekomposisi matriks
adalah memodifikasi atau merubah matriks menjadi matriks segitiga bawah (L)
dan/atau matrks segitiga atas (U), sehingga:
A = LU maka didapat, Det(A) = det(L) det(U)
Dalam menghitung dekomposisi matriks ada beberapa metode, diantaranya:
1. 1. Metode crout, metode ini digunakan untuk
mendekomposisi matriks yang menghasilkan elemen diagonal utama dari matriks
segitiga atas U adalah satu.
2. 2. Metode doollite, metode ini digunakan
untuk mendekomposisi matriks yang menghasilkan elemen diagonla utama matriks
segitiga bawah L adalah satu.
1. 3. Metode Cholesky, metode ini digunakan
untuk endekomposisi matriks diagonal utama L dan U sama. Metode ini hanya untuk
matriks yang simetris.
4. Metode operasi elementer, metode ini
digunakan untuk mendekomposisi matriks menjadi segitiga atas atau segitiga
bawah
Contoh
soal determinan matrik menggunakan metode dekomposisi matrik :
Dekomposisi
matriks berikut menjadi matriks segitiga bawah (L) dan segitiga atas (U).
5. Metode Doolittle :
INVERS MATRIKS
PENGERTIAN :
Invers matriks adalah sebuah kebalikan (invers) dari kedua
matriks di mana apabila matriks tersebut dikalikan menghasilkan matriks persegi
(AB = BA ). Simbol dari invers matriks adalah pangkat -1 di atas hurufnya.
Contoh matriks B adalah invers matriks A ditulis B = A–1 dan matriks A adalah
invers dari matriks B ditulis A = B-1. Matriks A dan B merupakan dua matriks
yang saling invers (berkebalikan). Invers matriks terdiri dari dua jenis yaitu
matriks persegi (2×2) dan matriks 3×3
TEKNIK MENGHITUNG INVERS :
·
Metode Adjoint Matrik
·
Metode Operasi Elementer Baris (OBE)
·
Metode Perkalian Invers Matrik Elementer
·
Metode Partisi Matrik
·
Program Komputer – MATCADS, MATLAB
·
WS OFICE EXCELL
A.
METODE ADJOINT MATRIK
·
Invers Matriks 3×3 Metode Adjoin
Adjoin
diperoleh dari transpose suatu matriks. Caranya mudah, yaitu diagonal utama sebagai sumbu putar.
Putar berlawanan arah jarum jam
dan didapatlah Adjoin.
Rumus Invers
Matriks :
Tentukan
invers matriks berikut ini menggunakan metode adjoint!
Penyelesaian
:
·
Invers Matriks 4 x 4 Metode Adjoin
Contoh soal :
B. Metode Operasi Baris Elementer ( OBE )
* Invers
Matrik Menggunakan Metode OBE
OBE adalah
salah satu alternatif dalam menyelesaikan suatu bentuk matriks seperti
menentukan invers matriks. Ada 3 langkah dalam menyelesaikan OBE, yaitu :
1. Mengalikan suatu baris bilangan
dengan bilangan bukan nol.
2. Menambah kelipatan suatu baris pada
baris lain.
3. Menukarkan sembarang dua buah baris
Ketiga langkah OBE tersebut hanya
bisa digunakan salah satunya saja.
Contoh Soal :
C. PERKALIAN MATRIKS ELEMENTER
Matrik elementer adalah matrik yang
diperoleh dari operasi elementer yang dikenakan pada matrik identitas. Setiap
matrik elementer mempunyai invers, dan setiap matrik bujur sangkar berordo
(nxn) yang mempunyai invers ekivalen baris terhadap matrik identitas I.
Matrik
elementer E diperoleh dari transformasi matrik identitas dimana pada kolom ke-I
diganti dengan normalitas vektor kolom :
Contoh Soal :
D. Metode Partisi
Adalah Metode yang digunakan untuk
menyelesaikan Invers matriks.
Untuk
mempermudah kita langsung ke contoh soal saja. Jadi disini saya memiliki sebuah
matriks berordo 3×3:
1. 1. Langkah pertama dalam mengerjakan
Metode Partisi adalah dengan menentukan A11,A12,A21 dan A2 dimana untuk
pembagiannya bisa menggunakan banyak cara tergantung dari yag mengerjakan soal.
2. mencari invers A22, hal ini
dikarenakan invers A22 akan digunakan di dalam rumus-rumus partisi selanjutnya.
3. Mencari Matriks B11 dengan rumus
Nah kita
tinggal mensubtitusikan nilai A11,A12,invers A22,dan A21. dan jalankan secara
matematis, namun don’t forget untuk menginverskan hasilnya lagi .
4. Mencari Matriks B12 dengan rumus
Nah kita
tinggal mensubtitusikan nilai B11,A12,dan invers A22. dan jalankan secara
matematis, namun jangan lupa untuk mengalikan hasilnya dengan (-) .
5. Mencari Matriks B21 dengan rumus
Nah kita tinggal mensubtitusikan nilai B11,A12,dan invers A22. dan
jalankan secara matematis, namun jangan lupa untuk mengalikan hasilnya dengan
(-) .
6. Mencari Matriks B22 dengan rumus
Nah kita
tinggal mensubtitusikan nilai B12,A21,dan invers A22. dan jalankan secara
matematis .
7. Terakhir subtitusikan Matriks B11,B12,B21,dan B22 pada matriks yang berordo 3x3.
setelah kita
subtitusikan didapatkan hasil dari invers dari matriks A.
SISTEM PERSAMAAN LINIER
Sistem
persamaan linear adalah sekumpulan persamaan linear yang terdiri dari beberapa
variabel. Contohnya adalah:
Sistem ini
terdiri dari tiga persamaan dengan tiga variabel x, y, z. Solusi sistem linear
ini adalah nilai yang dapat menyelesaikan persamaan ini. Solusinya adalah:
X = 1
Y = -2
Z = -2
Contoh
sistem linear yang paling sederhana adalah sistem linear dengan dua persamaan
dan dua variabel:
2x + 3y = 6
4x + 9y = 15
Salah satu
cara untuk menyelesaikan sistem tersebut adalah dengan mengubah persamaan
pertama menjadi seperti ini:
Kemudian
masukkan nilai x ke dalam persamaan kedua:
Hasilnya
adalah satu persamaan dengan satu variabel saja, yaitu y. Dari persamaan ini
diketahui bahwa y=1 dan y bisa dimasukkan ke dalam persamaan pertama untuk mencari
x. Hasilnya adalah x=3/2.
Bentuk umum
Sistem
persamaan linear m dengan n yang tidak diketahui dapat ditulis seperti ini
Cara
menyelesaikan SPL bisa menggunakan beberapa metode :
·
Metode
Eliminasi Gouss
·
Metode
Eliminasi Gouss Jourdan
·
Metode
Crammer
·
Metode
Invers Matrik
·
Metode
Dekomposisi Matrik
·
Metode
Gouss Seidel
·
Metode
Jacobi
·
Metode
Numerik
·
Solusi
dengan program komputer
·
METODE
ELIMINASI GOUSS
maka x = 1, y= 2, z=3.
·
METODE
ELIMINASI GOUSS JOURDAN
·
METODE
CRAMMER
Aturan
Cramer adalah rumus untuk mencari penyelesaian sistem persamaan linear dengan
memakai determinan suatu matriks dan matriks lain yang disusun dengan mengganti
salah satu kolom dengan vektor yang terdiri dari angka di sebelah kanan
persamaannya. Sebagai contoh:
NILAI EIGEN DAN VEKTOR EIGEN
Dalam
Aljabar Linear, Nilai Eigen () adalah nilai karakteristik dari suatu matriks
berukuran n x n, sementara vektor Eigen adalah vektor kolom bukan nol yang bila
dikalikan dengan suatu matriks berukuran n x n akan menghasilkan vektor lain
yang memiliki nilai kelipatan dari vektor Eigen itu sendiri.
Persamaan
karakteristik dari matriks A adalah persamaan dengan variabel lamda yang digunakan untuk
perhitungan nilai dan vektor Eigen. Polinomial karakteristik f(λ) adalah fungsi
dengan variabel λ yang membentuk persamaan karakteristik. Persamaan
karakteristik bisa diperoleh lewat cara berikut:
Contoh Soal dan Pembahasan :
1. Jika A =
tentukan
eigen dan vektor eigen dari matriks tersebut!
Jawab : det
(A-Iλ) = 0, mencari eigen :
( A-Iλ )
2. Tentukan nilai dan vektor eigen dari matriks!
Diagonalisasi
langkah-langkah menentukan matrik P dan D adalah :
1. Hitung persamaan karaketristik A nilai eigen
2. Carilah n vektor eigen bebas linier A sesuai nilai eigen,P1,P2,...Pn,
3. Bentuklah matrik P = [P1,P2,...Pn] dan hitunglah P invers
4. Hitung D = Pinvers.AP dengan diagonal utama, 𝞴1,𝞴2,...𝞴n.
Contoh soal :

ORTOGONALISASI MATRIK
Matriks Ortogonal adalah matriks persegi yang inversnya sama dengan transpos. Baris-baris pada matriks ortogonal membentuk himpunan ortonormal. Dengan kata lain, baris-barisnya adalah vektor satuan, di mana hasil kali titik (dot product) antara dua baris berbeda adalah nol.
Matriks persegi A disebut Matriks Ortogonal jika invers dari matriks A sama dengan transposnya. Dengan kata lain, hasil kali antara matriks A dengan transposnya adalah matriks identitas.
Berdasarkan definisi, matriks ortogonal pasti invertible (punya invers) dan inversnya adalah transpos dari matriks tersebut.
Aksioma 1:
Jika ¯u dan ¯v adalah objek dalam V, maka ¯u+¯v juga berada dalam V.
Catatan: Aksioma ini mungkin telah dipandang umum sebagai sifat ketertutupan operasi penjumlahan.
Aksioma 2:
¯u+¯v=¯v+¯u
Catatan: Aksioma ini mungkin telah dipandang umum sebagai sifat komutatif penjumlahan.
Aksioma 3:
¯u+(¯v+¯w)=(¯u+¯v)+¯w
Catatan: Aksioma ini mungkin telah dipandang umum sebagai sifat asosiatif penjumlahan.
Aksioma 4:
Ada objek ¯0 dalam V yang disebut objek nol (selanjutnya vektor nol), sedemikian sehingga berlaku
¯0+¯u=¯u+¯0=¯u
untuk setiap u∈V.
Catatan 1: Aksioma ini mungkin telah dipandang umum sebagai bentuk identitas penjumlahan.
Catatan 2: Objek ¯0 yang disebut sebagai “identitas” tidak selalu berarti vektor nol ¯0=(0,0,⋯,0). Hal ini tergantung dari definisi operasi yang diberikan. Jika diberikan himpunan A, maka untuk a∈A, haruslah berlaku
a∗¯0=a
Prinsip seperti ini sebenarnya sama dengan prinsip pada identitas penjumlahan/perkalian bilangan real, yaitu untuk a∈R,
a+0=a dan a×1=a
Untuk itu, 0 disebut identitas penjumlahan dan 1 disebut identitas perkalian pada bilangan real.
Aksioma 5:
Untuk setiap ¯u∈V, ada objek −¯u∈V yang disebut negatif dari ¯u sedemikian sehingga berlaku
¯u+(−¯u)=(−¯u)+¯u=¯0
Catatan 1: Aksioma ini mungkin telah dipandang umum sebagai invers penjumlahan.
Catatan 2: −¯u juga tidak selalu sama dengan −¯u=(−u1,−u2,⋯,−uk). Hal ini tergantung dari operasi yang diberikan. Suatu vektor dikatakan invers dari vektor yang lain jika keduanya dioperasikan menghasilkan identitas. Untuk itu, identitasnya harus terlebih dahulu diketahui.
Aksioma 6:
Jika k adalah sembarang skalar dan ¯u adalah sembarang objek dalam V, maka berlaku k¯u∈V.
Catatan: Aksioma ini mungkin telah dipandang umum sebagai sifat ketertutupan operasi perkalian.
Aksioma 7:
k(¯u+¯v)=k¯u+k¯v
Catatan: Aksioma ini mungkin telah dipandang umum sebagai sifat distributif perkalian terhadap penjumlahan.
Aksioma 8:
(k+m)¯u=k¯u+m¯u
Catatan: Aksioma ini mungkin telah dipandang umum sebagai sifat distributif perkalian terhadap penjumlahan.
Aksioma 9:
k(m¯u)=(km)¯u
Catatan: Aksioma ini mungkin telah dipandang umum sebagai sifat asosiatif perkalian.
Aksioma 10:
1¯u=¯u
Catatan: Aksioma ini mungkin telah dipandang umum sebagai bentuk identitas perkalian.
contoh soal :
Kita perlu
memeriksa keberlakuan cukup 1 saja aksioma ruang vektor.jika 1 aksioma sudah
terbukti maka benar.
Dengan demikian, V adalah ruang vektor real.
Subruang/Subspace/Ruang
Bagian
Misalkan V adalah ruang vektor dan W adalah
himpunan bagian dari V . Himpunan W disebut subruang dari
V , jika W merupakan ruang vektor di bawah operasi penjumlahan
vektor dan perkalian skalar yang didefinisikan pada V .
CONTOH SOAL
Kombinasi Linear
Misalkan V adalah ruang
vektor dan v1,v2 adalah dua vektor dalam V. Pada V berlaku operasi penjumlahan
dan perkalian dengan skalar. Artinya, kita dapat mengalikan v1 dan v2 dengan skalar,
sebutlah k dan m, sehingga terbentuk
vektor kv1 dan mv2. Dengan menjumlah
kedua vektor, diperoleh kv1+mv2. Nah, vektor ini
disebut sebagai kombinasi linear dari v1 dan v2.
Sebagai contoh, salah satu kombinasi
linear dari (1,2) dan (0,3) adalah 2⋅(1,2)−1⋅(0,3)=(2,1). Kombinasi linear lainnya adalah 0⋅(1,2)+2⋅(0,3)=(0,6).
Berdasarkan definisi, vektor w disebut
kombinasi linear dari v1,v2,…,vr jika kita dapat menemukan skalar-skalar k1,k2,…,kr yang memenuhi
persamaan vektor
w=k1v1+k2v2+…+krvr
contoh soal :
Akibatnya, solusi sistem persamaan di atas adalah k1=−3 dan k2=2. Dengan demikian, w adalah kombinasi linear dari u1 dan u2.
Kebebasan Linear
Jika S = { v1 ,
v2 , … vr } adalah himpunan vector, maka
persamaan vektor
k1v1 + k2v2 +……+
krvr = 0
mempunyai paling sedikit satu pemecahan
k1 = 0
k2 = 0
kr = 0
Jika ini adalah satu-satunya pemecahan, maka S kita namakan himpunan bebas
linear (linearly independent). Jika ada pemecahan lain, maka S
kita namakan himpunan tak - bebas linear (linearly
dependent)
Contoh
soal:
Tentukan apakah himpunan berikut ini
bebas linear?
1) S = { (2,1,1) , (3,1,0) , (2,1,-3) }
Jawab:
S = { (2,1,1) , (3,1,0) , (2,1,-3) }
k1v1 + k2v2 +……+
krvr = 0
menjadi
k1(2,1,1) + k2(3,1,0) + k3(2,1,-3)
= (0,0,0)
(2k1 + 3k2 + 2k3 ,k1 + k2 + k3 ,k1 -
3k3) = (0,0,0)
didapat SPL
2k1 + 3k2 + 2k3 =
0
k1 + k2 + k3
= 0
k1
- 3k3 = 0
Karena determinan dari matriks tersebut adalah 4
dengan aturan cramer, maka didapat k1 = 0/4 , k2 =
0/4, dan k3 = 0/4.
Jadi persamaan tersebut mempunyai satu-satunya
pemecahan yaitu k1=k2=k3 = 0 maka S bebas Linear.
BASIS DAN DIMENSI
Basis : suatu ukuran tertentu yang menyatakan komponen dari sebuah vector. Dimensi biasanya dihubungkan dengan ruang, misalnya garis adalah ruang dengan dimensi 1, bidang adalah uang dengan dimensi 2 dan seterusnya. Definisi basis secara umum adalah sebagai berikut :
Jika V adalah ruang vektor dan S = {v1, v2, v3, ….., vn} adalah kumpulan vektor di dalam V, maka S disebut sebagai basis dari ruang vektor V jika 2 syarat berikut ini dipenuhi :
i. S bebas linier; ii. S serentang V.
CONTOH :
TENTUKAN BASIS DAN DIMENSI DARI RUANG VEKTOR YANG DIBENTUK OLEH :
A = [1,2,3] B = [2,4,6] C = [2,3,5]
JAWAB :
misal : p = [p1,p2,p3]
p = q1A+q2B+q3C
(p1,p2,p3)=q1(1,2,3)+q2(2,4,6)+q3(2,3,5)
(p1,p2,p3)= q1+2q2+2q3, 2q1+4q2+3q3, 3q1+6q2+5q3
q1+2q2+2q3=p1
2q1+4q2+3q3=p2
3q1+6q2+5q3=p3
jika membangun det MK tidak samadengan 0.
TRANSFORMASI LINEAR

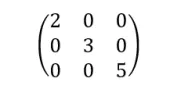




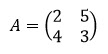














































































































Komentar
Posting Komentar